Calculator: 37 Tips For Writing Polynomials In Standard Form

Today’s topic is Writing Polynomials In Standard Form Calculator. Obviously, you can find a great deal of Polynomial Calculator-related content online. The proliferation of online platforms has streamlined our access to information.

There is a connection between the Quadratic To Standard Form Calculator and Expanded Polynomial In Standard Form Calculator information. additional searching needs to be done for Polynomial Factored Form To Standard Form Calculator, which will also be related to Writing Polynomials In Standard Form Worksheet.

37 Things About Writing Polynomials In Standard Form Calculator | Precalculus

• For polynomials whose coefficients come from more abstract settings (for example, if the coefficients are integers modulo some prime number p, or elements of an arbitrary ring), the formula for the derivative can still be interpreted formally, with the coefficient ka k understood to mean the sum of k copies of a k . For example, over the integers modulo p, the derivative of the polynomial xp + x is the polynomial 1.[17] - Source: Internet
• Combine like terms to add two polynomials. To combine similar terms, the terms must contain the exact same variables with the same degrees. To subtract two polynomials, add the first polynomial and the negative (or opposite) value of the second polynomial. - Source: Internet
• The polynomial calculator calculates the value of a variable for a given polynomial. The standard form of a polynomial refers to writing a polynomial in a diminishing power of a variable. What is a polynomial equation calculator? - Source: Internet
• For polynomials in one variable, there is a notion of Euclidean division of polynomials, generalizing the Euclidean division of integers.[e] This notion of the division a(x)/b(x) results in two polynomials, a quotient q(x) and a remainder r(x), such that a = b q + r and degree(r) < degree(b). The quotient and remainder may be computed by any of several algorithms, including polynomial long division and synthetic division.[14] - Source: Internet
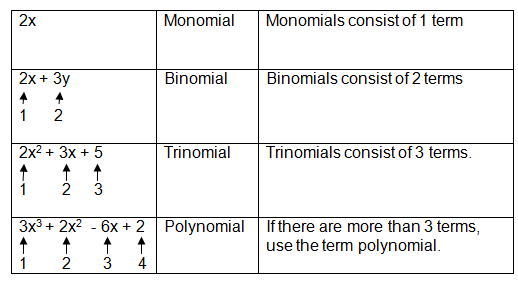
• Polynomials are sums of terms of the form k⋅xⁿ, where k is an arbitrary number and n is a natural number. For example, 3x + 2x5 is a polynomial. Introduction to polynomials. This video covers common terminology such as terms, degree, standard form, monomial, binomial, and trinomial. - Source: Internet
• (If you have a graphing calculator, you can pre-screen the rational roots by graphing the polynomial and seeing where it seems to cross the x axis. But you still need to verify the root algebraically, to see that g(x) is exactly 0 there, not just nearly 0.) - Source: Internet
• Formal power series are like polynomials, but allow infinitely many non-zero terms to occur, so that they do not have finite degree. Unlike polynomials they cannot in general be explicitly and fully written down (just like irrational numbers cannot), but the rules for manipulating their terms are the same as for polynomials. Non-formal power series also generalize polynomials, but the multiplication of two power series may not converge. - Source: Internet
• Standard polynomial form (polynomials in standard form) refers to writing a polynomial in diminishing powers of a variable. Let’s understand this concept with an example. Write the polynomial 5 + 2x + x 2 in standard form. To represent the above polynomial in standard form, first check the degree of the polynomial. - Source: Internet
• Determining the roots of polynomials, or “solving algebraic equations”, is among the oldest problems in mathematics. However, the elegant and practical notation we use today only developed beginning in the 15th century. Before that, equations were written out in words. For example, an algebra problem from the Chinese Arithmetic in Nine Sections, circa 200 BCE, begins “Three sheafs of good crop, two sheafs of mediocre crop, and one sheaf of bad crop are sold for 29 dou.” We would write 3x + 2y + z = 29. - Source: Internet
• Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. - Source: Internet
• In this example, cubic polynomials are used. Standard monomials (1, x, x 2, x 3) are often used as base functions for regression. (Here a base in a linear-algebraic sense is used to denote the base of a vector space). - Source: Internet
• If R is an integral domain and f and g are polynomials in R , it is said that f divides g or f is a divisor of g if there exists a polynomial q in R such that f q = g. If a ∈ R , {\displaystyle a\in R,} then a is a root of f if and only x − a {\displaystyle x-a} divides f. In this case, the quotient can be computed using the polynomial long division.[24][25] - Source: Internet
• Calculating the volume of polynomials involves the standard volume solution equation and basic algebraic arithmetic using the First-Last-Inner-Outer (FOIL) method. Note the basic formula for volume: volume = length_width_high. Plug the polynomials into the volume formula. Example: (3x + 2) (x + 3) (3x^22). - Source: Internet
• Plug the polynomials into the volume formula. Use the First Last Internal External (FOIL) method to multiply the first two equations. A more detailed explanation of the FOIL method can be found in the References section. Multiply the last given equation (which you didn’t win) by the new equation you won. - Source: Internet
• and such that the degree of r is smaller than the degree of g (using the convention that the polynomial 0 has a negative degree). The polynomials q and r are uniquely determined by f and g. This is called Euclidean division, division with remainder or polynomial long division and shows that the ring F is a Euclidean domain. - Source: Internet
• A polynomial is called a standard form if the terms of an expression are ordered from highest to lowest degree. Standard form makes it easy to find the degree of a polynomial. What do you have to do to write a polynomial in standard form? Steps to write polynomials in standard form:. - Source: Internet
• There are some rules about what polynomials cannot contain: Polynomials cannot contain division by a variable. For example, 2y 2 + 7x / 4 is a polynomial because 4 is not a variable. However, 2y2 + 7x / (1 + x) is not a polynomial because it contains division by a variable. Polynomials cannot contain negative exponents. - Source: Internet
• Some polynomials, such as x2 + 1, do not have any roots among the real numbers. If, however, the set of accepted solutions is expanded to the complex numbers, every non-constant polynomial has at least one root; this is the fundamental theorem of algebra. By successively dividing out factors x − a, one sees that any polynomial with complex coefficients can be written as a constant (its leading coefficient) times a product of such polynomial factors of degree 1; as a consequence, the number of (complex) roots counted with their multiplicities is exactly equal to the degree of the polynomial. - Source: Internet
• Polynomials can also be multiplied. To expand the product of two polynomials into a sum of terms, the distributive law is repeatedly applied, which results in each term of one polynomial being multiplied by every term of the other.[7] For example, if - Source: Internet
• If sin(nx) and cos(nx) are expanded in terms of sin(x) and cos(x), a trigonometric polynomial becomes a polynomial in the two variables sin(x) and cos(x) (using List of trigonometric identities#Multiple-angle formulae). Conversely, every polynomial in sin(x) and cos(x) may be converted, with Product-to-sum identities, into a linear combination of functions sin(nx) and cos(nx). This equivalence explains why linear combinations are called polynomials. - Source: Internet
• A polynomial with 1 as degree of a polynomial is called a linear polynomial. Linear polynomials can have multiple variables. So they see a linear polynomial in one variable as a kind of polynomial in one variable. Examples x + 7, 3y - 27, 7z + 17/2. - Source: Internet
• Because of their strict definition, polynomials are easy to use. So you can add and multiply a lot and end up with a polynomial. Also, single-variable polynomials can easily be graphed because they have smooth, solid lines. - Source: Internet
• The ambiguity of having two notations for a single mathematical object may be formally resolved by considering the general meaning of the functional notation for polynomials. If a denotes a number, a variable, another polynomial, or, more generally, any expression, then P(a) denotes, by convention, the result of substituting a for x in P. Thus, the polynomial P defines the function - Source: Internet
• When there is no algebraic expression for the roots, and when such an algebraic expression exists but is too complicated to be useful, the unique way of solving it is to compute numerical approximations of the solutions.[20] There are many methods for that; some are restricted to polynomials and others may apply to any continuous function. The most efficient algorithms allow solving easily (on a computer) polynomial equations of degree higher than 1,000 (see Root-finding algorithm). - Source: Internet
• Both polynomials have zeroes at 1 and 4 only. f(x) has degree 3, which means three roots. You see from the factors that 1 is a root of multiplicity 1 and 4 is a root of multiplicity 2. Therefore the graph crosses the axis at x = 1 (but is not horizontal there) and touches at x = 4 without crossing. - Source: Internet
• Remember that r is a root if and only if x−r is a factor; this is the Factor Theorem. So if you want to check whether r is a root, you can divide the polynomial by x−r and see whether it comes out even (remainder of 0). Elizabeth Stapel has a nice example of dividing polynomials by long division. - Source: Internet
• With quadratics, we were able to algebraically find the maximum or minimum value of the function by finding the vertex. For general polynomials, finding these turning points is not possible without more advanced techniques from calculus. Even then, finding where extrema occur can still be algebraically challenging. For now, we will estimate the locations of turning points using technology to generate a graph. - Source: Internet
• There are several rules about what polynomials cannot contain: Polynomials cannot contain division by a variable. For example, 2y 2 + 7x / 4 is a polynomial because 4 is not a variable. However, 2y2 + 7x / (1 + x) is not a polynomial because it contains division by a variable. Polynomials cannot contain negative exponents. There cannot be 2 + 7x4 for 2 years. - Source: Internet
• In Mathematics, a polynomial is defined as an algebraic expression that consists of different terms, variables, coefficients, constants and non-negative integer exponents. Also, different arithmetic operations can be performed on polynomials such as addition, subtraction, multiplication and division. A polynomial can be of different types, namely - Source: Internet
• For polynomials with more than one indeterminate, the combinations of values for the variables for which the polynomial function takes the value zero are generally called zeros instead of “roots”. The study of the sets of zeros of polynomials is the object of algebraic geometry. For a set of polynomial equations with several unknowns, there are algorithms to decide whether they have a finite number of complex solutions, and, if this number is finite, for computing the solutions. See System of polynomial equations. - Source: Internet
• Note the basic formula for volume: volume = length_width_high. Plug the polynomials into the volume formula. Use the First Last External Internal (FOIL) method to multiply the first two equations. - Source: Internet
• In the case of polynomials in more than one indeterminate, a polynomial is called homogeneous of degree n if all of its non-zero terms have degree n. The zero polynomial is homogeneous, and, as a homogeneous polynomial, its degree is undefined.[c] For example, x3y2 + 7x2y3 − 3x5 is homogeneous of degree 5. For more details, see Homogeneous polynomial. - Source: Internet
• The calculation of the volume of polynomials involves the standard volume solution equation and elementary algebraic arithmetic using the First-Last-Inner-Outer (FOIL) method. Note the basic formula for volume: volume = length_width_high. Plug the polynomials into the volume formula. - Source: Internet
• Symbolic Roots If you have Symbolic Math Toolbox™, then there are additional options for evaluating polynomials symbolically. One way is to use the solve (Symbolic Math Toolbox) function. syms x s = solve(x^2-x-6) s = -2 3 Another way is to use the factor (Symbolic Math Toolbox) function to factor the polynomial terms. F = factor(x^2-x-6) F = [ x + 2, x - 3] See Solve Algebraic Equations (Symbolic Math Toolbox) for more information. - Source: Internet
• You can also divide polynomials (but the result cannot be a polynomial). The degree of a polynomial in a variable is the largest exponent of that variable. For more complex cases, read the degrees (expressions). - Source: Internet
• The polynomial 0, which may be considered to have no terms at all, is called the zero polynomial. Unlike other constant polynomials, its degree is not zero. Rather, the degree of the zero polynomial is either left explicitly undefined, or defined as negative (either −1 or −∞).[5] The zero polynomial is also unique in that it is the only polynomial in one indeterminate that has an infinite number of roots. The graph of the zero polynomial, f(x) = 0, is the x-axis. - Source: Internet
• To divide two polynomials, do the following: Order the divisor and dividends in descending order of their degrees. Divide the first term of the dividend by the first term of the divisor to get the first term of the quotient. Find the product of all the terms of the divisor and the quotient of the first term and subtract the result from the dividends. - Source: Internet

Following are some suggestions for where to begin your search for data on Writing Polynomials In Standard Form Worksheet: You should try to find SAT Total Prep 2022: 2,000+ Practice Questions + 5 Practice Tests-related information from reputable places. Libraries, online resources, and even paid journalists all fall under this category. - It's crucial to be aware of the various electronic media sources available when researching write polynomial in standard form with the given zeros calculator, such as Google and YouTube. You may also get info about Polynomial on social media sites like Facebook and Twitter.

It’s crucial to read to examine the authenticity of each source in order to acquire the greatest information regarding Polynomial.

Video | Writing Polynomials In Standard Form Calculator

You’ll learn more about Rewrite In Standard Form Calculator after watching the films included in this post, which come from a variety of different sources. Information on a wide range of topics can be easily accessed via the internet.

## Notable features of College Algebra include:

• Writing Polynomials In Standard Form Calculator
• Write Polynomial In Standard Form Calculator
• Write Polynomial In Standard Form With The Given Zeros Calculator
• Rewriting Polynomials In Standard Form Calculator
• Write A Simplified Polynomial Expression In Standard Form Calculator

With the abundance of Vertex Form Calculator-related resources available online, it’s easy to find what you’re looking for.

This is not how most people would expect to learn more about Polynomial Coefficient Calculator, so be prepared for some shock value. It paves the way for a closer examination of the Select a Web Site information’s actual substance and its potential applications. techniques for making Rewrite The Following Polynomials In Standard Form data visualizations that are both aesthetically pleasing and practically applicable. They can spread the word about Rewrite In Standard Form Calculator in professional and promotional settings. For this reason, we also include Fraction Polynomial In Standard Form-related pictures.

At last, this article sums up key points about Polynomial. There is also a comparison of your Algebra II: Polynomials knowledge to that of Microsoft Math Solver, as well as a discussion on Writing Polynomials In Standard Form Worksheet and Precalculus.